
Bernoulli's ideas and equations work well with wings of the type of wing we are using when it is at ~5° of attack angle (Zero attack angle means lift force is zero). What happens though when the angle of attack is increased?
Before addressing this let us take a look at Newton’s Third Law which states: “For every action there is always an equal and opposite reaction”
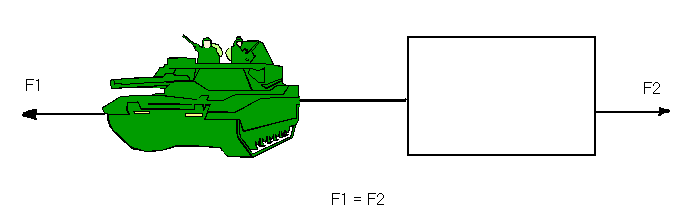
If the above tank pulls on the stationary crate with force F1 the crate will pull in the opposite direction with an equal force F2.
How does this apply to the under side of the wing? (What happens on the top side of the wing as the angle of attack increases will be discussed in Stall Stuff)
The knee-jerk response is to say that it is deflection and then to draw the following diagram:
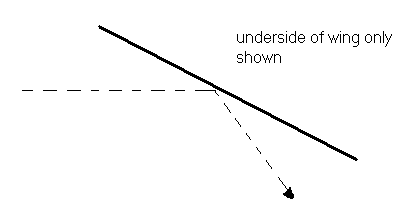
Dotted line represents air flow
This picture violates the candle demo though (see Bernoulli) in that this picture does not show the air forming a boundary layer. a more accurate picture is as follows:
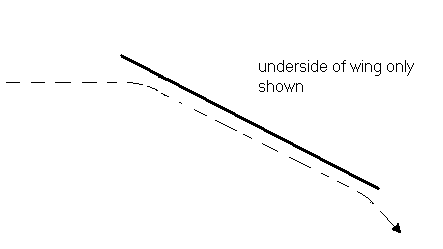
Dotted line represents air flow
Forcing the air to flow like this will generate more lift force than when the wing was at an angle of ~5°.
Demonstration
To show this, set the wing at an angle of 30° on the protractor on the cart (not on the vertical protractor). For the construction of the general apparatus see Construction of Demonstration. Attach the spring and hold the cart (spring unstretched). Turn the wind generator on and pull on the spring to make sure the cart always stays in the same place. The length that the spring stretches can be used to give an idea of relative forces as F = -kx. Note the length of the spring. This length will be longer and we can conclude that the force is greater here.