In class, we calculate an estimate the back-EMF produced by a motor with a 6-turn square coil, when it is spinning at its maximum frequency, and when one arm of the coil is at its closest position to the magnet.
We make the following simplifying assumptions:
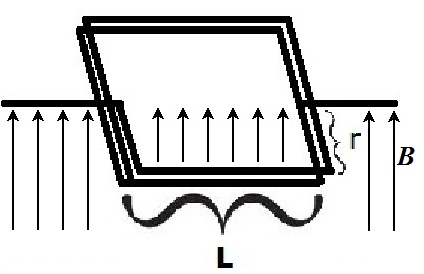
This gives us the following picture:
To derive a formula for the back EMF, we start with the equation for the magnetic force on a charge:
Dividing both sides by the charge, q, gives the magnetic force per unit charge:
If the force acts over a distance D, then the work per unit charge is:
This has units of Joules per Coulomb (J/C). That is, it has units of Voltage. This formula gives us the voltage induced by motion with velocity v through a magnetic field B. With this formula, we can calculate the voltage induced accross the lower arm of the coil as it rotates through the magnetic field. This is the back-EMF:
The angle θ between v and B at this point in time is π/2, by the assumption of constant B, so sinθ = 1. v = 2π*f*r, where f is the frequency of the motor's rotation in Hz. D = n*L, where L is the length of the arm of the coil and n is the number of turns. Making these substitutions, we obtain:
The magnetic field B was measured before the demonstration at the point where the coil is closest to the magnet. If the values of L and r are given in meters, then B should be given in Teslas. L and r were measured with a ruler. n, the number of coil turns, was recorded when the coil was wound. f was measured in class using a stroboscope.
By multiplying all these values together, we obtain our estimate for the peak back-EMF.
This is only the peak back-EMF. A time-averaged back-EMF for the entire cycle could be obtained by integrating over θ. In addition, the assumption of constant B will not hold well at other points in the rotation; the field strength drops off rapidly as the arm of the coil moves away from the magnet, so this must be taken into account.