UNDERSTANDING THE CORIOLIS FORCE
University of British Columbia
Department of Physics
In any rotating reference frame, such as the Earth, a merry-go-round or a spinning ice skater, an observer sees a new influence on the motion of objects. A ball thrown between two friends on a merry-go-round will appear to them to take a curved path. They are spinning with the merry-go-round, while the ball moves freely through the air. The force that causes this curvature of motion in the rotating reference frame is the Coriolis force. It always points perpendicular to the object’s velocity.
This famous force is most widely associated with large-scale phenomena, especially in meteorology. However, the Coriolis force is named after a French mathematician who worked in a very different field. Gaspard Gustave Coriolis’ (1792-1843) most famous paper was entitled “On the equations of relative motion of a system of bodies,” and an earlier paper was called “On the principle of kinetic energy in the relative motion in machines.” Coriolis is credited with extending the concepts of work and energy to the rotating reference frame and applied his research to machines such as waterwheels.
What is the Coriolis Force?


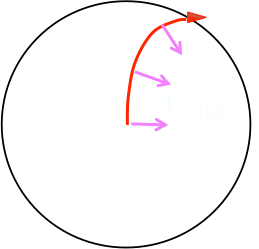
Deflection of Moving Objects
Table Rotating CCW
One simple example of the Coriolis force has been observed at least as early as 1651. Italian military officers wrote that in artillery practice their cannon balls always landed to the right of where their calculations predicted. Their observations were correct. The cannon ball was shot over such a long distance that while it was in the air, the Earth rotated underneath it. Since these officers were in Italy they saw the cannon balls curve to the right (Earth rotates counter clockwise in the northern hemisphere).
Earth is a rotating reference frame. This is why the Coriolis force can be observed acting on a cannon ball (as long as it is shot over a sufficiently large distance). There are countless other examples of the Coriolis force acting on Earth. In fact, it is crucial to creating the conditions on Earth that we take for granted. Some of the major instances of the Coriolis force on Earth are discussed under the “Rotating Earth” section of this website.
Quantifying the Coriolis Force
From a rotating reference frame, any object in motion will be influenced by the Coriolis force. Its strength depends on only a few variables, and the relative direction of their vectors. First of all, the object’s linear (tangential) velocity must be considered. Only the component of velocity that is perpendicular to the rotating frame’s axis of rotation contributes to the Coriolis force. Angular velocity, then, is also a factor in the equation for the Coriolis force. In particular, one must determine the cross product of linear velocity and angular velocity. The final factor in the Coriolis force is the mass of the object.
Image: Persson. (1998). Bulletin of the American Meteorological Society, 79(7). 1373-1385.
Gaspard Gustave Coriolis (1792-1843) was a French mathematician. He generalized the concepts of work and energy to rotating systems.

The vector equation for the Coriolis force is shown above. The underlined and bolded characters are vectors whose magnitudes and directions must be considered. As mentioned, the cross product between rotational velocity (omega) and linear velocity (v) multiplies only the vector components that are orthogonal. The result of the cross product is orthogonal to both v and Ω. Its direction can be determined by the right hand rule. Take your right hand and orient your index finger, middle finger and thumb as shown below.
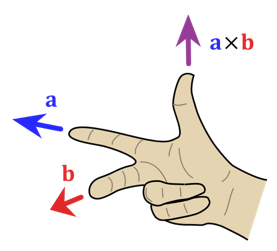
The Right Hand Rule for Cross Products
In the case of the Coriolis force, your index finger (blue) points in the direction of the object’s velocity. Your thumb (purple) points in the direction of the axis of rotation. Your middle finger (red) will then point in the opposite direction of the resulting Coriolis force. This is indicated by the negative sign in the equation above.
The Right Hand Rule for Rotation Axis
If you are unsure which direction Ω points, you can use a different version of the right hand rule. This time make a loose fist, but keep your thumb extended. Let the curl of your fingers point in the direction of rotation, then your thumb will point in the direction of the angular velocity, Ω.

It is now clear that the Coriolis force is observed only in the rotating reference frame. Where, then, does the energy for this force come from? How can energy be conserved between the rotating and non-rotating reference frames?
Gaspard Gustave Coriolis’ understood his work on rotating systems in terms of rotational kinetic energy. Meteorologists and other scientists who followed Coriolis attempted to understand his work in terms of only linear velocity or only angular velocity. They were unable to derive the formula shown above. Instead they came up with F=-mΩv (one half of the correct formula). This is because energy is conserved in both linear and angular metrics. The correct derivation of the formula requires angular momentum and linear momentum. Furthermore, if there is any interaction between the rotating reference frame and the object (friction, air resistance, etc...) then only the energy of the system (object and reference frame) will be conserved.
Another useful fact to consider is that the Coriolis force can do no work. Therefore, it does not “use up” any energy from the reference frame. The energy transfer implied in the paragraph above only contributes to the force of friction. The Coriolis force still exists when there is no friction. No work can be done by the Coriolis force because it always points perpendicular to the object’s motion. A standard concept in kinematics is that work is only done by a force when the force points in the same direction as the object’s velocity that it is acting on.
What about Conservation of Energy?
University of British Columbia
Department of Physics
Tony Battistel
December 2012
