UNDERSTANDING THE CORIOLIS FORCE

The Coriolis force can be easily demonstrated on a simple rotating table. A camera co-rotating with the table can capture the rotating reference frame, and provide a very clear visualization of the Coriolis force on an object. On the right are the trajectories of a marble on a spinning table from the rotating frame (top) and stationary frame (bottom).

Images: http://montshire.org/images/uploads/ex-spin-table.jpg

Learning about the Coriolis force on a spinning table (2D) is much easier than trying to understand how it works on a three-dimensional globe. On a spinning table objects can only roll around, and are restricted to motion in a plane that is perpendicular to the axis of rotation. This guarantees that the object’s velocity is perpendicular to Ω (the axis of rotation) and simplifies the formula for the Coriolis force to the scalar equation shown below.

University of British Columbia

Department of Physics

Tony Battistel

December 2012

The Coriolis force is often explained through many examples. However, most examples require first hand experience to really understand. Demonstrating the Coriolis force on a spinning table is a sure way to convince anyone that it plays a significant role in the rotating reference frame, yet doesn’t exist at all in the stationary frame. This can be shown undisputedly through the use of a video camera: roll a marble over the surface of the spinning table and record one video from the rotating frame and one from the stationary frame. Students are always surprised by the video recorded on the camera that is rotating with the table. This camera has captured the rotating reference frame and shows the marble taking an almost circular path due to the Coriolis force.

These are the rough trajectories for a marble on a counter-clockwise rotating table in the stationary frame (left) and rotating frame (right). Of course, for a table with friction, the straight line in the stationary frame would be slightly deflected to the left (CCW rotation). In the rotating frame, friction would only reduce the curvature of shown trajectory. Here is a link to my video demonstration.

The Coriolis force always points perpendicular to the velocity of the object it is acting on. On a counter-clockwise rotating table (or any surface) it points 90º to the right. On a clockwise rotating table it points 90º to the left. Anyone who has studied circular motion should know that this (circular motion) is exactly what the Coriolis force should produce, and it does! If the spinning table were infinitely large the rotating camera would show the marble circling around forever (and slowly moving away from the rotation axis due to centrifugal force). Centrifugal force, however, depends on friction between the object and the rotating frame whereas the Coriolis force exists with or without friction.

In the trajectory from the rotating frame (shown above right), friction is working against the Coriolis force, because the table is rotating CCW. But friction works in conjunction with the Coriolis force for part of the trajectory too (it is not shown in the picture above). The force of friction from the table always points in the tangential direction.

Motion due to the Coriolis force in a spinning bowl is even more fascinating than the motion it causes on a flat surface. Since the marble can’t roll out of the bowl (assuming your bowl isn’t rotating at extreme speeds) you can observe its behavior longer. In fact, if you get the right bowl you may be able to balance the centrifugal force perfectly with the pull of gravity into the center of the bowl. Then you will be able to see the Coriolis force extremely clearly, with only friction to distort its influence. However, you can get great results with any smooth bowl. The difference in the trajectories from the two reference frames is much more significant than on the flat surface.

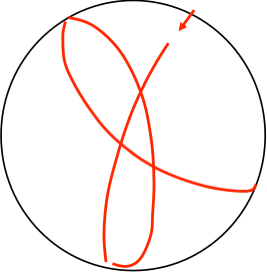
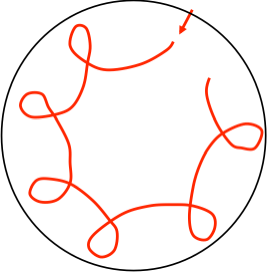
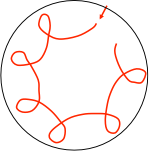
These are the rough trajectories for a marble in a counter-clockwise spinning bowl from the stationary reference frame (left) and the rotating reference frame (right). The time over which each trajectory is drawn is not equal (less time for stationary frame). The Coriolis force pushes to the right, and friction pulls along the tangent to the circle. Here is a link to my video demonstration.

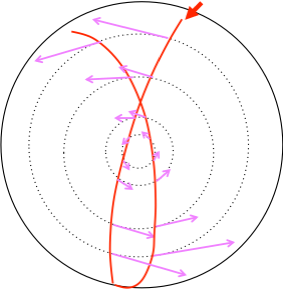
In the stationary frame, the marble rolls back and forth exchanging gravitational potential energy for kinetic energy. While it does so, friction from the spinning bowl drags its path along. Thus the angle of the trajectory precesses around the bowl due to friction. All the same forces are present in the rotating reference frame in addition to the Coriolis force. The Coriolis force (again) always pushes objects to the right in CCW rotating frames. The circular motion it produces is clearly shown in the image above on the right. The Coriolis force causes the small clockwise circles while friction causes the larger scale counter-clockwise precession of these small circles. The force of friction and the Coriolis force on the marble are shown below for each reference frame.

Showing the influence of the Coriolis force is easy when you have a rotating table with a mounted camera! And it’s easy to build such an apparatus by yourself if you’ve used some basic tools before. Step by step instructions are provided in the “Build a Demo” page of this website. This demonstration provides first-hand experience with the Coriolis force. Not only that, but the distinction between friction, gravity and Coriolis can be much more easily accounted for and calculated on a spinning table. Anyone with basic math skills can use the scalar equation to find the Coriolis force on the marble. Plus the experimenter can change the table’s rotation rate, the object’s velocity and use objects of different masses, which allows direct manipulation over each variable affecting the Coriolis force. The demonstration is very powerful and great for an introduction to the Coriolis force.

The Coriolis force and force of friction are shown at each point on the marble’s trajectory for the stationary frame (left) and the rotating frame (right). Coriolis force is shown in black and friction is shown in pink. The bowl is rotating counter-clockwise.

If there was no friction in the bowl, the motion would be different. The oscillations in the stationary frame would no longer be distorted by friction, and the trajectory would be perfectly straight. The spinning bowl would have no influence on the marble (other than the normal force of course). In the rotating frame, a marble moving in a frictionless bowl produces beautiful circular motion. The lack of friction means the small Coriolis circles seen directly above will not precess around the bowl - they will stay in the exact same spot. It also means that the marble will never lose energy (nothing is lost in the exchange between potential and kinetic because there is no friction), so it will move in circles forever in the rotating frame. The trajectories for a marble in a rotating frictionless bowl are shown below.

These are rough trajectories for a marble in a frictionless rotating bowl shown from the stationary reference frame (left) and rotating reference frame (right). In the stationary frame we see perfect linear motion, and in the rotation frame we see perfect circular motion.