Resonance in Wind Instruments

This demonstration aims to introduce students to concept of resonance in the context of sound waves. This demonstration is designed for the more specific context of musical wind instruments in order to make it clear to students how the mathematical properties of sound waves correspond to the familiar properties of sound; frequency is pitch, amplitude is volume, and spectrums of frequencies combine to form other properties such as tone.

The physical setup of the demonstration consists of several pipes, which approximate a wind instrument. By varying the length, material, and shape of the pipes, and by varying how we make sound from them, we can control what pitch is made by the pipes. This is used to demonstrate resonance as the main mechanism for amplifying the sound of the pipes.

Lesson

What is sound? Put simply, sound is a wave of pressure in a medium. When you clap your hands, for example, you create an area of compressed air. The increased pressure between your hands then pushes on the air around your hands, moving the area of high pressure away from the initial clap without actually moving the air away from your hands on average; this front of high pressure is followed by a front of lower pressure, as momemtum pulls some pressure away. If we were to graph this pressure difference against time, we would get a sine function:

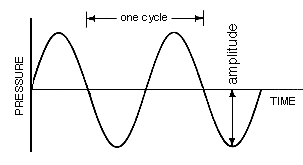
The length of a single cycle in time is called the period "T". Most sounds don't create a single wave front, but many; the rate at which these waves pass is called the frequency "f". If we look at the pressure difference against position instead of time, then the length of a single cycle is the wavelength "λ"; λ is the distance that the wave moves in a single period T. We can relate these quantities together using the speed of sound, which in roughly 343 meters per second:

v=d/t=λ/T=λf

This means that if we know the wavelength of sound wave, then we also know the frequency (so long as the medium is air, and the temperature and humidity are normal for an interior room).

What is resonance? Resonance is the combination of overlapping waves as they are reflected within a medium. When you have a space such as a pipe which reflects sound waves at both ends, the combination of these waves resonates to create standing waves; standing waves with fixed nodes composed of two waves moving in opposite directions:

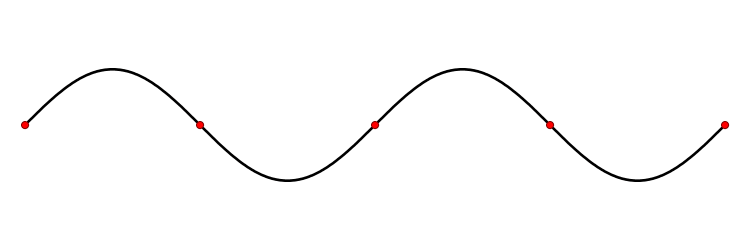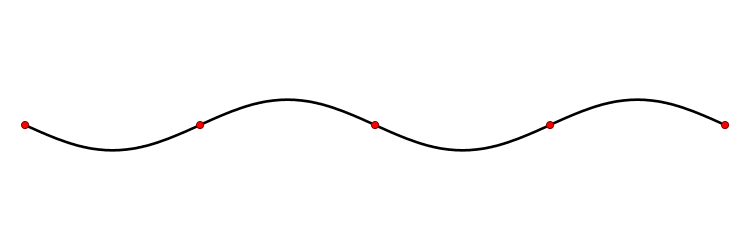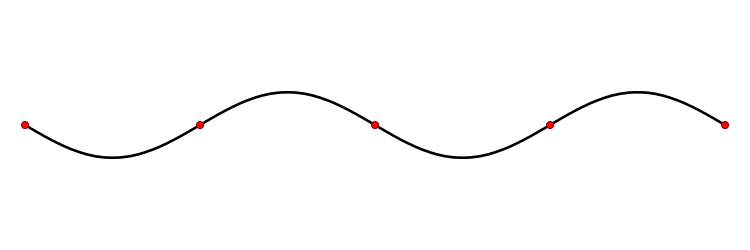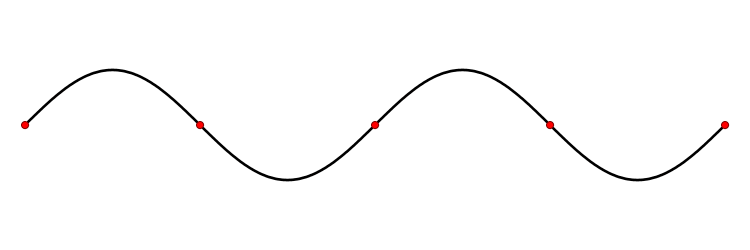
Nodes in a sound wave, seen above as red dots, are places in the wave that are at atmospheric pressure. The points midway between nodes where the wave is at the highest or lowest are called antinodes.

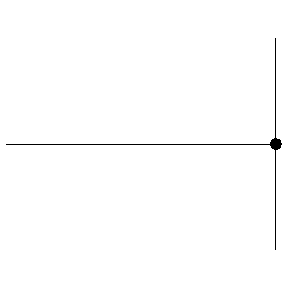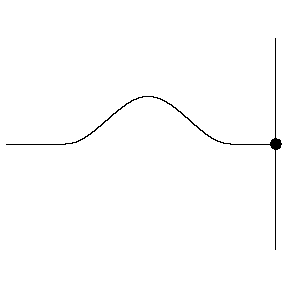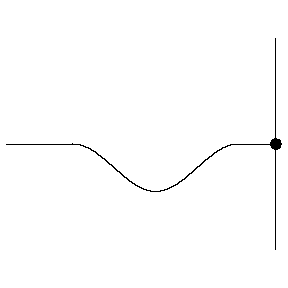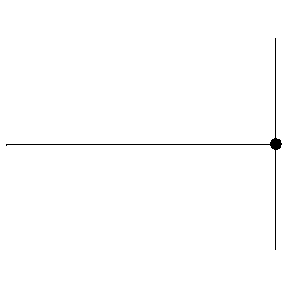
In order to understand how resonance happens in instruments, we need to first understand how sound waves are reflected in instruments. Whenever a sound wave reaches a change of medium, part of the wave continues into the new medium, and part of the wave is reflected back. When is is significantly harder for sound to move through the new medium, most of the wave is reflected, and the phase (positive or negative sign) is reversed:

When the wave is not moving into a medium that requires more energy to move through, most of the wave continues, and the smaller reflected waves preserves phase:

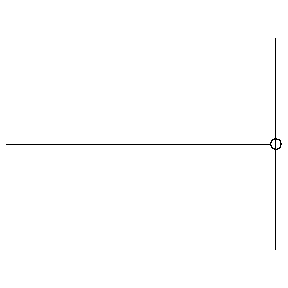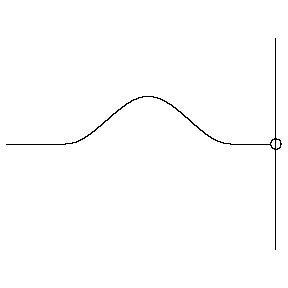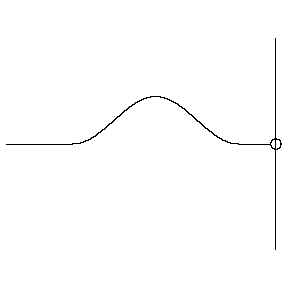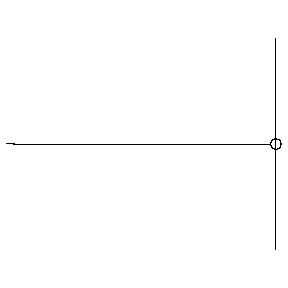
This phase of reflection allows us to predict the wavelength of waves reflected in a pipe. At open ends, which experience the softer phase-preserving reflection, the incoming and reflected waves share a phase, and therefore combine to increase amplitude at the open end. This creates an antinode. At closed ends, which experience the harder phase-reversing reflection, the incoming and reflected waves have opposite phases, and so they cancel out. This creates a node. Therefore, only waves which have antinodes at open ends and nodes at closed ends can resonate in a pipe.

Using this observation, we can find the frequencies of sound that resonate for a given pipe. For a pipe with both ends open, we require an antinode at both ends, so given the sine function shape, the length of the pipe must be a multiple of half the wavelength: length=nλ/2 n=1, 2, 3...

For a pipe with one open end and one closed end, the length of the pipe can be a quarter of the wavelength plus a multiple of half the wavelength; length=nλ/2+λ/4 n=0, 1, 2...

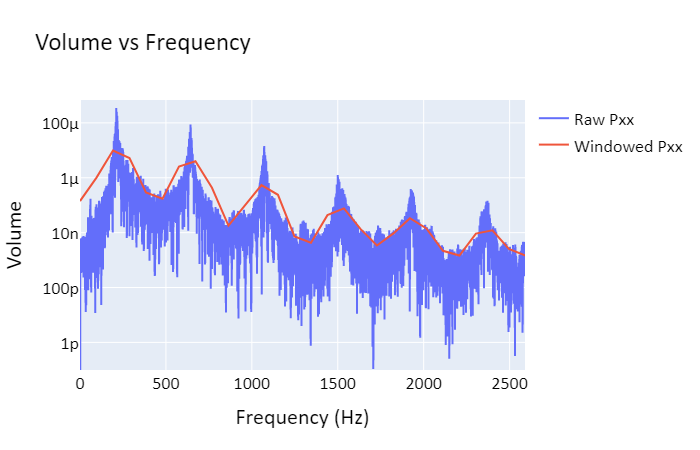
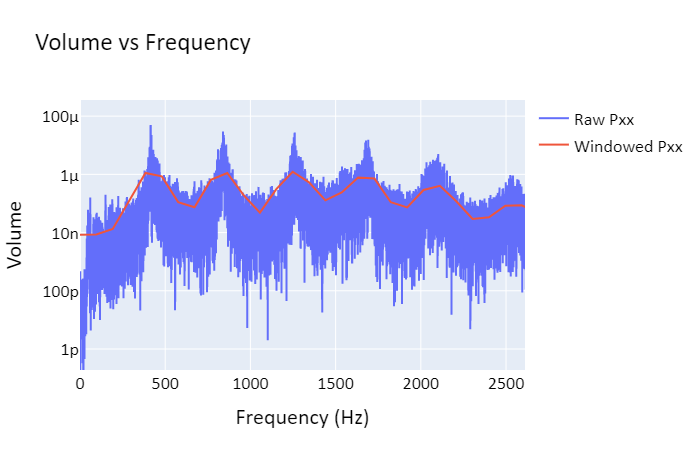
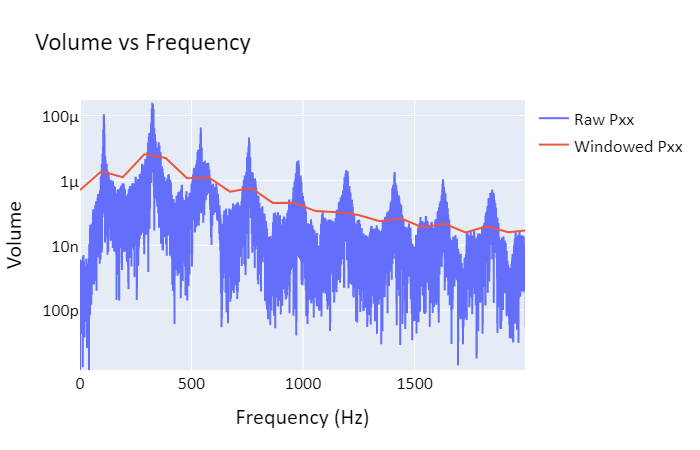
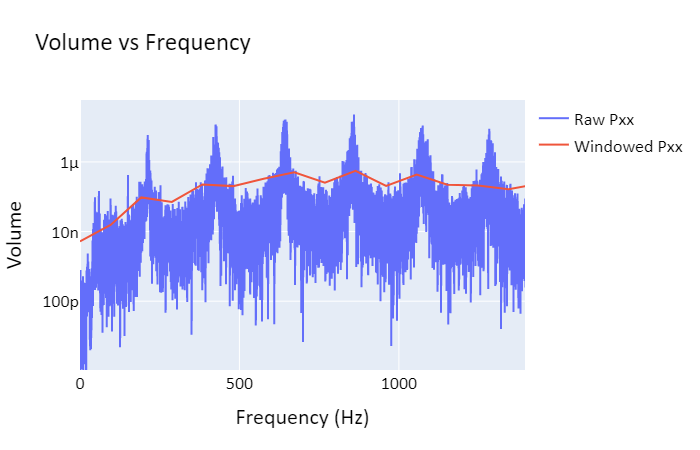
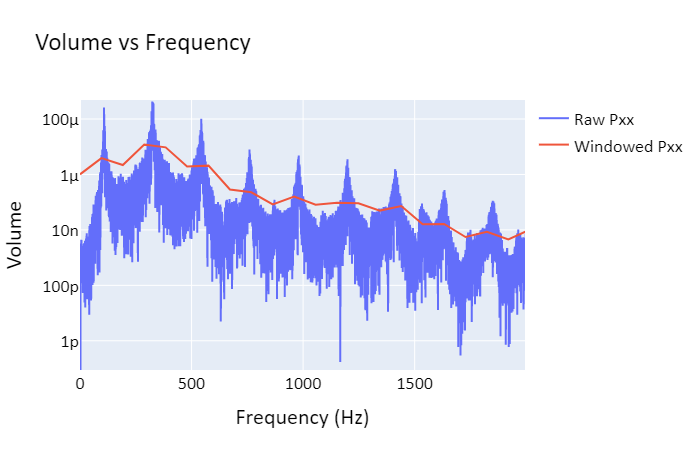
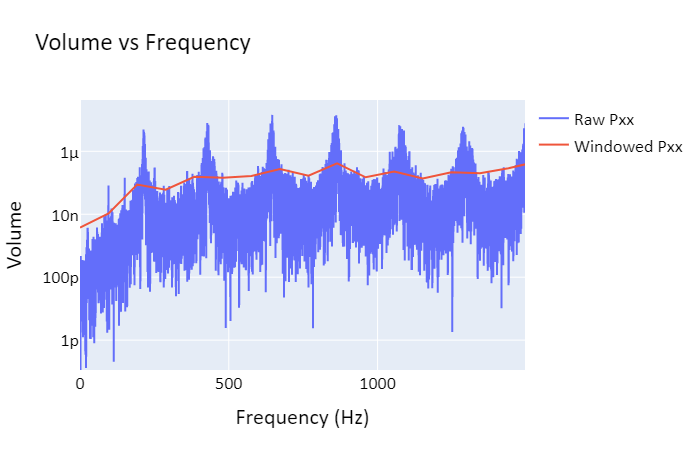
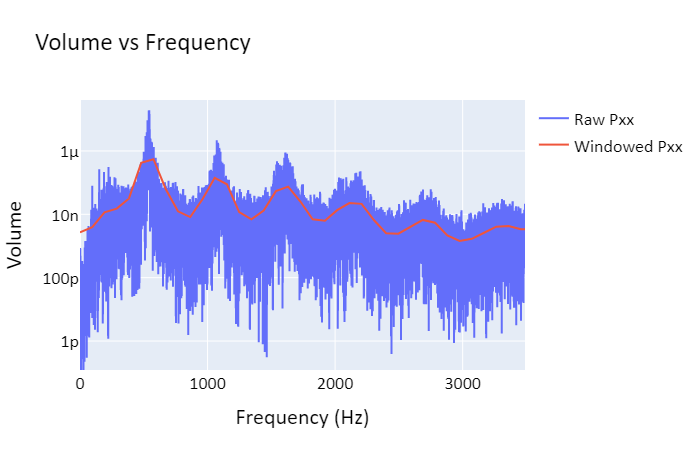
Note that lower frequencies are prefered due to their lower energy. Combining this with the equations above, we find that the main pitch created by an open/open pipe, called the fundamental frequency, is f=v/(2L). For an open/closed pipe, the fundamental frequency is f=v/(4L).

Holes in a pipe function similarly to an open end in creating antinodes; most real wind instruments work either by opening and closing holes to effectively control the length of the instrument (woodwinds), or by opening and closing valves in order to control the length of the instrument (brass). Instruments using open/open end resonance include the flute and certain pipe organs, while open/closed end resonance is used in instruments such as clarinets and trumpets. This distinction between open and closed resonance explains why clarinets are lower in pitch than flutes despite having similar lengths.

Here are the slides used in the classroom presentation of the demonstration:

Construction

The demonstration consists of various pipes, used to verify the predictions about frequency made above. Measuring equipement, preferably either a meter stick or a tape measure, will be needed for both construction and presentation of the demonstration, since the point of the demonstration is the relationship between the length of the pipes and the pitch of the sounds made.

First, a note on method. Any given pipe can be "played" in one of two ways. If struck cleanly with the palm on one end, so that the palm of the hand completely covers the opening, you should get a clean note; this is the result of open/closed resonance, with the hand closing one end. To acheive open/open resonance, the end can be struck in such a way as to avoid covering the end, or air can be blow across the top as one would blow across the opening of a flute.

The first two pipes are plastic pipes of varying lengths. PVC pipes can be bought and cut relatively cheaply at many hardware stores. The reason we want two different lengths of pipe is to demonstrate qualitatively that a shorter pipe produces a higher pitch. If the shorter pipe is half the length of the higher pipe, then it can also be shown qualitatively that open/open end resonance has the same pitch as an open/closed end pipe with half half the length. This is significant because it allows a demonstration of the principles before pitch is even measured. I would suggest 39.0cm for one of the two pipes, as it's fundamental frequency is the A note in the A440 tuning system. Choosing a second pipe to be twice the length (78.0cm) is prefered over a shorter pipe since a larger pipe resonates more clearly.

The third pipe is the same length as one of the first two pipes, but is made from metal instead of plastic. This pipe can be used to illustrate the fact that the sound is coming from resonance in air rather than a direct amplification of the initial disturbance. First, strike both the plastic and metal pipes on the side to show that the material creates a very different sound, then play the two different material pipes as described above; the played sound should be nearly identical.

The fourth pipe is conical rather than cylindrical; it gets wider from one end to the other. This pipe is 3D-printed, and is as long as the 3D-printing permits. If an especially long 3D-printer is available, printing the conical pipe to share a length with the shortest cylindrical plastic pipe allows for direct comparison. The wider opening should be wider by between a third and a half. The purpose of this pipe is to demonstrate how the conical versus cylindrical shapes affect the distribution of overtones in the produced sound; overtones are the resonant frequencies above the fundamental.

The fifth pipe is a plastic pipe similar to the first two, except that it has a hole in it. This demonstrates the mechanism used by most woodwind instruments to control the pitch: adding a hole effectively changes the length of the pipe, and covering the hole changes the effective length back to the full length. Note that the resonant frequencies of both sides will be present to a certain extent, though the side struck will be dominant. The distorting effect of the two distinct resonant spectrums can be hidden by putting the hole at the midpoint, giving both sides of the hole the same resonant spectrum.

Finally, the frequency must be measured. Many phone apps can be used to view a spectrum of frequencies, graphing the volume of the sound against its frequency. I used an app named Spectroid available on the Google Play store, but any verified frequency spectrum analysis tool will work. Using such a spectrum analysis tool, you will be able to see the dominant frequencies, which should closely align with the predicted resonant frequencies with the fundamental being the largest. For the conical pipe, the fundamental should dominate more greatly, with the higher resonant frequencies falling off.

Demo

In order to convey some part of the demonstration, I've included recordings of the open and closed resonance of each of the mentioned pipes. Each recording is accompanied by a frequency spectrum analysis of the recording; note that the exact volume is not important, as the only aspect of the volume we are interested in are the location of the peaks in the frequency domain.

39.0cm pipe closed resonance

Given the equations worked out above, we can predict that a 39.0cm pipe with open resonance should have a fundamental frequency of f=343/(4*0.390) Hz=220. Hz, which is supported by the measurement of frequency. Furthermore, we can see higher resonance frequencies every 440 Hz above the fundamental, as expected.

39.0cm pipe open resonance

Here, we can see that, as expected, the open resonance frequencies for the 39.0cm pipe are 440 Hz, and every 440 Hz above.

78.0cm pipe closed resonance

78.0cm pipe open resonance

It is important to compare the 78.0cm open pipe resonance to the 39.0cm closed pipe resonance, since they should share a fundamental frequency by not the rest of their frequency spectrum. Try listening to them back to back; do they sound like the same note despite the difference in tone?

78.0cm metal pipe closed resonance

Listen to the metal pipe and 78.0cm plastic pipe recordings back to back. Can you tell the difference? If you cannot tell them apart, that's good: they should have an identical frequency spectrum.

78.0cm metal pipe open resonance

Conical pipe closed resonance

Note that for the conical pipe, the higher resonances fall away quickly compared to the cylindrical pipes, where the second resonance is often as strong or stronger than the fundamental.

Conical pipe open resonance