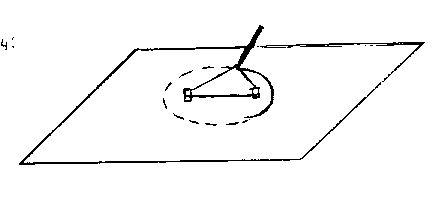
An ellipse is one of the conic shapes, which also include the parabola, the hyperbola, and the circle. The conics are called conics because if you take a cone, and slice it in different ways, you will get the shapes of the various conic sections. If you take a circular hoop, turn it on an angle, and close one eye, the shape you will see is an ellipse. Another interesting demonstration of an ellipse is to take a piece of paper, and tape or glue two short posts onto it, about eight centimeters apart. You could use flat-headed thumb tacks, and stick them with their flat tops against the paper, and the pins pointing straight up. Then take a piece of string, and tie it into a loop, about 26 centimeters in circumference. Put the loop around both of the pins, and stretch it out to one side. Put a pen on the paper where the loop is stretched out. Keeping the string under tension between the three points (two pins and the pen), move the pen around the pins for a full 360 degrees. The resulting shape is an ellipse. This drawing also demonstrates a fundamental concept about the geometry of an ellipse: the sum of the distances from each focus to any point on the ellipse is a constant.
Diagram 4: drawing an ellipse

Diagram 5: parts of an ellipse
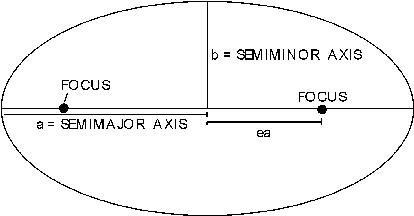
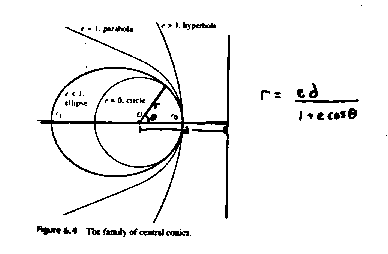
An ellipse consists of a semi-major axis (a), which is the distance from the center of the ellipse to the furthest point away from the center, and a semi-minor axis (b), which is the distance from the center of the ellipse to the closest point away from the center. The ellipse has two foci, two points that are located along the semi-major axis at equal distances from the center. Their location depends on the eccentricity (e) of the ellipse. The eccentricity is a measure of how elliptical (how far from a circle) the ellipse is. The eccentricity may have values ranging from zero to one, for an ellipse. If the eccentricity is zero, the ellipse is simply a perfect circle, with both foci in the same place, in the center of the circle. If the eccentricity is exactly one, the ellipse is not closed, and it is a parabola instead, with one focus located at infinity. If the eccentricity is greater than one, the path is a hyperbola. In more advanced math, it can be shown that all of the conics can be related by one formula, where the eccentricity is the only variable determining which conic it will be.
Diagram 6: the family of conics
An interesting note at this point is that Kepler came up with the word "focus" for these points in the ellipse, which is Latin for "fireplace". Kepler found that the Sun (the big fireplace in the sky) is at one focus of the elliptical orbit of Mars.