(from Between Copernicus and Galileo by James Lattis)
Johannes Kepler was born in Germany eight years after Galileo was born. He was an exceptional mathematician, and was offered refuge from religious persecution by an astronomer named Tycho Brahe. Tycho was known for his excellent measurements, and when a supernova erupted in 1572, he became famous for proving that this new star was farther away than the Earth's atmosphere, and even than the planets. He was granted great wealth and resources by the king for his discovery. He used his personal island observatory and team of assistants to take very accurate measurements of the heavens for about thirty years.
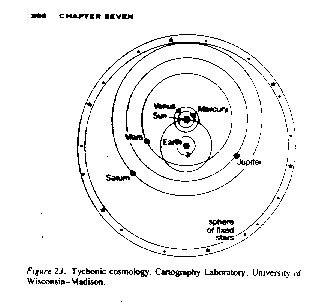
Tycho hired Kepler to analyze his data, hoping to prove that his own planetary system was the correct one. Tycho's system was very similar to the Ptolemaic system, except that he put Venus and Mars circling the Sun as the Sun circled the Earth. He also added a sphere of stars around the outside of the system, which is where he thought the stars stay, fixed in their place.
Diagram 3: Tychonian system

The problem was that Kepler was an avid supporter of Copernicus, not of Ptolemy or Tycho. Luckily (for Kepler), Tycho died shortly after they began working together, and Kepler inherited Tycho's job and data. Imagine Kepler's problem: all of the data had been collected from a moving post, on the planet Earth, which orbits around the Sun along some unknown path, and the observations are of another planet also orbiting the Sun along some unknown path. This is where Kepler's mathematical genius came in handy. Kepler did a very complete and detailed analysis of the data, and in the end, came up with an unexpected result.
Kepler's system did have the Sun in the centre, and all of the planets orbiting around the Sun, and the Moon orbiting around the Earth. However, there were no longer any epicycles, and instead of uniform circular motion, the planets were now given elliptical paths. The data fit the theory precisely: it was the best system yet. Incidentally, it is worth noting that it was pure luck that Kepler chose to analize the data for the orbit of Mars, which has a more elliptic orbit than most planets. He worked on Mars because that is what Tycho's principle assistant was working on at the time when Kepler started working for Tycho. If Kepler had chosen another planet, he probably would have ended up staying with circular orbits and epicycles.
Kepler summarized his findings in three laws. Kepler's First Law states:
K I: The planets orbit around the Sun in an elliptical orbit, with the Sun at one focus.
Think about uniform circular acceleration for a moment. If you have two planets orbiting the same star at different radii (distances) from the star, which one must move faster to maintain it's orbit?
So now we know that a planet that is further away from the Sun does not have as great a speed as the closer planet has. If you think about an ellipse with the Sun at one focus, do you think the planet will have a constant speed as it orbits the Sun, or should the speed of the planet vary, depending on its distance from the Sun?
The answer is that its speed varies with its distance from the Sun. In fact it moves much faster when it is close to the sun than when it is far from the sun. If you watch a ball rolling around in a gravity well, you will see that it speeds up when it loops around the central hole (which represents a heavy mass, or the Sun), and it slows down when it gets far away from the central hole.
This leads up to Kepler's second law. When the ball is going slowly (when its radius from the sun is large), it travels a shorter distance in a given time interval than if it is moving fast (when it's radius from the sun is small).
So, for a given time period, dt, a slow speed (small v) corresponds to a small distance traveled (small ds).
If we choose a time period, and mark the distance the planet travels around the ellipse in that time, we will get a short curved line if we measure it when the planet is far from the Sun, and a long curved line if the planet is close to the Sun. The length of the line is the distance the planet traveled in that time period. If we then connect the end of each line segment to the focus (the Sun), we will get a triangular area with a curved top. Kepler found that if you calculate the area of this curved triangle, you will get the same area every time (using the same ellipse and the same time interval). So if the planet is far from the Sun and it's line segment is short, it's radius will sweep out the same area as will be swept out when the planet is close to the Sun and it's line segment is long. This is Kepler's Second Law, also known as the Law of Equal Areas:
K II: If a line is drawn from the Sun to the planet, the line sweeps out equal areas in equal time intervals.
Kepler's third law states:
K III: The squares of the sidereal periods (P) of the planets are proportional to the cubes of the semimajor axes (a). (A sidereal period is the period for one complete orbit).
Diagram #10: planetary data
PERIOD SEMIMAJOR AXIS ECCENTRICITY
Square Cube
PLANET T(yrs) T²(yrs²) a(AU) a³(AU³) e
--------------------------------------------------------------------
Mercury 0.241 0.0581 0.387 0.0580 0.206
Venus 0.615 0.378 0.723 0.378 0.007
Earth 1.000 1.000 1.000 1.000 0.017
Mars 1.881 3.538 1.524 3.540 0.093
Jupiter 11.86 140.7 5.203 140.8 0.048
Saturn 29.46 867.9 9.539 868.0 0.056
Uranus 84.01 7058 19.18 7056 0.047
Neptune 164.8 27160 30.06 27160 0.009
Pluto 247.7 61360 39.44 61350 0.249
--------------------------------------------------------------------
Notice that Kepler's third law suggests a proportionality, not an equality between the square of the period and the cube of the semi-major axis. In the above table the units have been carefully chosen so that a constant in the equality would just be one.
Then P² = ka³, where k is a constant.
If other units had been chosen for the period and the semimajor axis, the constant would not equal one. Can you think of any other units of measurement that could be chosen to yield a constant of one? (So that the square of the period and the cube of the semimajor axis would still be equal for each planet, even though the numbers would be different from the numbers in the table above).
Kepler proposed another theory to justify the distances of the planets from the Sun, and the number of planets (which was thought to be six in Kepler's time). There were five perfect solids known to people. A perfect solid is a 3-dimensional shape on which every face has exactly the same size and shape. These include the cube, tetrahedron, dodecahedron, icosahedron, and octahedron. Kepler proposed that by placing a sphere around each shape, and then placing one sphere inside another shape in a specific order, one would get a system which roughly modeled the solar system. The ratio of the radii of the spheres was approximately equal to the ratio of the radii of the planetary orbits.
Diagram #11: Perfect Solids theory

This theory actually has no physical basis, and it was dismissed by physicists long ago. So why did I tell you about it? To show that theories are just theories, not absolute truth. Even great physicist can make mistakes. And even great coincidences, such as the one Kepler found here, can just be coincidences. So just as Kepler and Galileo questioned the accuracy of the old Earth-centered model, other scientists questioned Kepler's models. His three laws were retained, but the perfect solid theory was dismissed. You'll be dismayed to hear that everything I have taught you about Kepler's laws is also false, in the context of our modern understanding of gravity. His laws are only true under a very special set of circumstances, and only to a limited degree of accuracy. This does not mean that the laws are useless; in fact they are still very useful for most calculations, but for very accurate calculations, more recent theories must be used.