Experiment on Kepler's Second Law

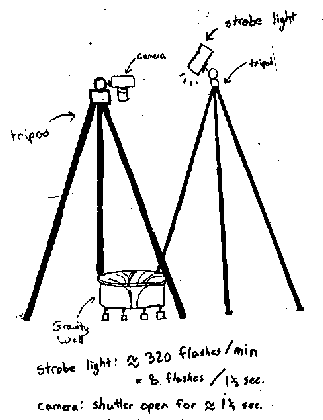
I decided to do a short experiment with a gravity well, to see if I could demonstrate Kepler's second law. I set up a camera directly over the gravity well, so that I could take pictures of it from above. I also put a strobe light on a tripod, close to the camera, so that the light would shine on the gravity well from above. I set the speed of the strobe light to about 320 flashes per minute, which works out to about 8 flashes every 1.5 seconds.

Diagram #7: Picture of the apparatus

I turned all of the lights off except the strobe light, and I set a large ball in motion, "orbiting" the hole in the center of the gravity well. I took pictures of the ball as it rolled around, and I kept the shutter open for about 1.5 seconds. Every time the strobe light flashed, it recorded a picture of the ball at a certain position in it's "orbit". Since the flash went off about eight times during each picture, I ended up with a picture of eight balls (or the same ball at eight different positions, separated by equal time intervals).

Diagram # 8: The photograph

Above is one of the photographs that I took. The small bright white spots are the reflections off the centre of the ball at each position it was in when the strobe light went off. The large white blotches are the reflections of light on the gravity well itself (which is made out of acrylic). The bean-shaped ring around a black patch is from refraction and reflection of light through the acrylic, and is caused because the light was not directly overhead, but off-set by a small angle. You can clearly see the rim around the outside of the well, and the hole in the center is marked by a small, 1/8 moon-shaped reflection around the edge of the hole.

I judged the centre of the hole and the centre of the reflection spots of the ball at different locations. I then measured the distances of the edges of three triangles, to see if the law of equal areas could be shown. I used calculus to determine the areas accurately, since one side of the "triangle" is curved. Calculus gives an accurate measure of the areas under curved lines. However, you could just as easily use the Law of Cosines to calculate the area of the triangle with straight edges. This will give an approximate answer. If you would like to try this, here is the Law of Cosines:

Diagram # 9: The Law of Cosines triangle

C² = A² + B² - 2ABcos(ø)

This can also be written as:
cos(ø) = (A² + B² - C²) / 2AB

You could also put the curved triangles over some graph paper, and count how many squares are inside each triangle to find the approximate area.

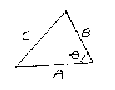
If I look at the results that I obtained using calculus (the most accurate method), I found areas (in square centimeters) of:

7.286

6.928

7.06

The areas are very similar. Of course, there are several sources of experimental error, which may account for the differences in values. For example, as a ball rolls around on acrylic, there is friction, with both the air and the acrylic. The ball will lose kinetic energy as a result, and so it will never move in a perfect ellipse; it will spiral in a bit before it completes the ellipse. Because of this friction, it eventually loses so much kinetic energy that the gravitational potential energy pulls it in towards the hole in the center. In reality, outer space is essentially a vacuum, so friction is not a problem: the planets can move in true elliptical orbits, without spiraling in to the Sun. There are also errors involved in judging the center of the ball and the hole on the photograph, and errors caused by the strobe light being slightly off-center (so the reflections will be off-center).

  • Main Menu

  • Back to Kepler