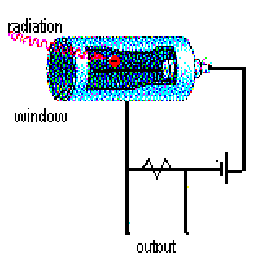
One way to detect radiation is to use an instrument called a Geiger counter. At the end of a Geiger tube is a window. Radiation passes through this window, and into the gas inside. At the other end of the tube is an electrode that is kept at a certain voltage. As the radioactive particles enter the Geiger tube, they excite a small voltage. This voltage is usually quite low. A device called a photomultiplier is often used to increase this small voltage to a more readable level. A photomultiplier works much like rolling a snowball down a hill. A small snowball with bump into other things and trigger an large snow slide if things are right. In this way, the Geiger counter is able to produce a measurable voltage that depends directly upon the number and intensity of the radioactive particles striking it. In addition to having a gage to read the radioactivity levels, often the counters make a beeping sound, whose frequency of beeps depends upon the radioactivity. The more beeps, the more radioactive something is.

If one had a large amount of time on their hands one could place a geiger counter next to a radioactive source to see what would happen with the passage of time. For most sources it would take a long time ( for uranium it would take on the order of a few million years), but one would see that the radioactivity levels would decrease with time. This fact is used in carbon dating. When a radioactive substance decays, it usually becomes more stable. Thus we expect there to be less decays (radiation) as a substance becomes more stable. Instead of waiting around a long time to see what happens to a substance, it is very convenient to express the relation of radioactivity and time with a mathematical equation. This has the advantage of letting us deal with a wide range of substances and determine radioactivity levels at any time without having to wait around. A nice way to see what this relation might be is to model the situation with some dice.
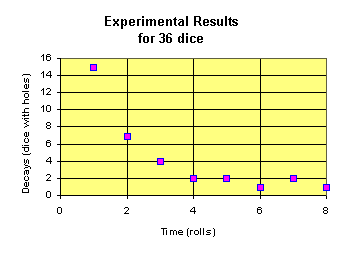
To simulate radioactive decay we have taken a large number of dice (36) and drilled a small hole through each die. We can imagine that each die represents a very simple radioactive element. Each radioactive element will have some chance that it will decay, emitting radiation. When a die lands showing the hole, we will assume that it has just emitted a radioactive particle. For simplicity we will assume that after this has happened, the particle is stable and will not react again. Doing this on an overhead makes it quite simple to see which dice have or have not emitted a radioactive particle. To see the relation that will develop, it is convenient to plot decays (dice with holes) vs. time (rolls). After each roll a point can be plotted on the overhead where the dice are rolled. The results show an exponential decay. This is what is expected. Exponential functions are often used to represent functions whose amount is dependent upon the amount immediately before. Population growth, bank interest (compounded continually) and radioactive decay are all some common usages of this function.
For our experiment the probability that any die will land with a hole is 1/3. This is because there are 6 sides to the die, 2 of which have holes. The relation we can determine from our dice demo can be given by
where R is the decay rate at any time, R0 is the initial decay rate, and t is time passed.
This expression can be generalized to incorporate different decay rates by simply changing the 1/3 to give
where r is a substance's decay rate.
This is the standard equation for radioactive decay. Often, a half life rather than decay rate may be listed for radioactive substances. A half life can be defined as the time is takes for the radioactivity to decrease to half its original amount. Doing a bit of math and some substitutions, we get
where l is called the half life of the substance.
As anyone who has been to a hospital knows, when one gets an x-ray, a lead cover is usually placed over areas not being exposed. Typically a lead vest is placed over the most sensitive organs. These shields are used to minimize to radiation dosage received by the patient. X-rays have a hard time passing through thick lead sheets. It possible to show this with a Geiger counter.
A small beta source such as cesium 137, can be measured with a Geiger counter. A few sheets of paper may be placed over the source and the radiation measured. Little if any difference may be noted. Next a piece of wood may also be placed over top. There should be a change in the radioactivity level. Finally a thick piece of steel or lead can be place over top. There should be little if any radioactivity measured.
